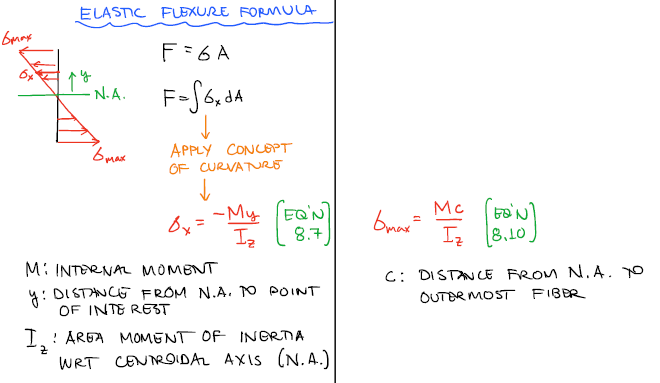
goglvision.blogg.se - Mechanics of materials flexture examples

#Mechanics of materials flexture examples free#

Strain e = ( δl / Original length) = ( PQ - P 1Q 1 ) / (PQ) The theory of bending is called theory of simple bending. This layer RS, which is neither compressed nor stretched, is known as neutral plane or neutral layer. The amount, by which a layer is compressed or stretched, depends upon the position of the layer with reference to RS. Now we see that the layers above RS have been compressed and that bellow have stretched. If we further proceed towards the lower layers are stretched the amount of extension increases as we proceed lower, until we come across the lowermost layer BD which has been stretched to B 1D 1. As we proceed towards the lower layer of the beam, we find that the layers have, no doubt, suffered compression, but to a lesser degree until we come across the layer RS, which has suffered no change in its length, through bent into R 1S 1. The top layer of the beam AC has suffered compression, and reduced to A 1C 1.

A little consideration will show, that all the layer of the beam, which were originally of the same length doing not remain of the same length any more. Since we are considering a small length of dx of the beam, therefore, the curvature of the beam, in this length, is taken to be circular. Due to the action of the bending moment, the beam as a whole will bend. Now consider two section AB and CD, which are normal to the axis of the beam RS.

The value of E(Young modulus of elasticity) is the same in tension and compressionĬonsider a small length dx of a simply supported beam subjected to a bending moment M.

#Mechanics of materials flexture examples free#

Each layer of the beam is free to expand or contract, independently, of the layer, above or below it.

The transverse sections, which were plane before bending, remain plane after bending also.

The beam materials are stressed within its elastic limit and, thus, obey Hooks law.

The material of the beam is perfectly homogeneous (i.e., of the same kind throughout) and isotropic (i.e., of equal elastic properties in all directions).

The following assumption is made in the theory of simple bending: An example of pure bending would be a beam with two couples, one on each end acting in opposite directions.ġ8.2 Assumption in the Theory of Simple Bending In contrast, non uniform bending refers to flexure in the presence of shear forces, which means that the bending moment changes as we move along the axis of the beam.

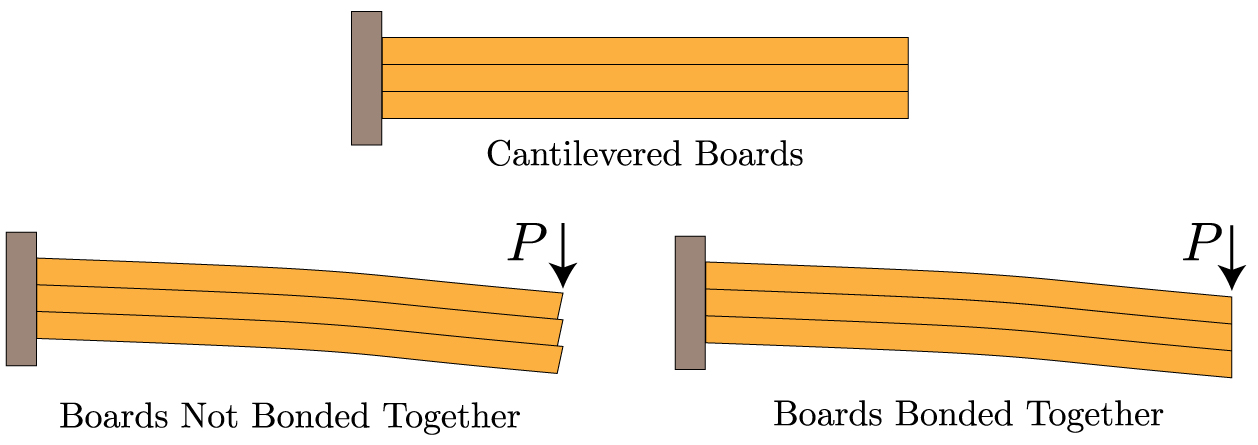
Therefore, pure bending occurs only in regions of a beam where the shear force is zero. Pure bending refers to flexure of a beam under a constant bending moment.